Eis que estava vendo alguns vídeos da categoria de Ciência da Computação no Khan Academy e alguns vídeos eram sobre os números de Fibonacci. Então, estou aqui para falar sobre Matemática e Programação, mais especificamente sobre os Números de Fibonacci. Ia postar o artigo em apenas uma parte, mas como me empolguei, dividirei em três duas partes:
- Fibonacci, Parte 1: A sequência de Fibonacci e os coelhos.
- Fibonacci, Parte 2: A Proporção Áurea.
Fibonacci, Parte 3 (final): Programação, o universo e tudo mais.
O número de Fibonacci e a população de coelhos
Não, eu não vou passar o número do telefone de Fibonacci. Até porque seu nome mesmo era Leonardo Pisano no Bigollo e viveu entre os anos 1170 e 1250 — tempo que não havia números de telefone. É também conhecido (ou não) como Leonardo de Pisa, Leonardo Pisano, Leonardo Bonacci, Leonardo Fibonacci, ou simplesmente, Fibonacci. A sequência de números foi apresentada em sua obra “Liber Abaci“, de 1202, na qual ele apresentava os chamados modus Indorum (método dos indianos), hoje conhecidos como Algarismos Arábicos. Tais números já eram conhecidos pela matemática indiana lá pelo século VI, mas foi Fibonacci o responsável por apresentá-los ao Ocidente.
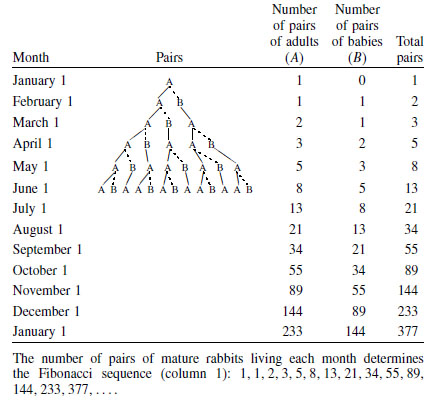
O problema utilizado por Fibonacci em Liber Abaci foi sobre o crescimento idealizado de uma população de coelhos. Para isso, era necessário que: um casal de coelhos fosse colocado num campo; cada casal amadurecesse sexualmente (e se reproduzisse) apenas após o segundo mês de vida; não houvesse problemas genéticos ou algo que impossibilitasse a fertilidade de cada casal; e que os casais nunca morressem, dando luz a um novo casal a cada mês, a partir do segundo mês de vida. O problema era: quantos pares (casais) de coelhos haveria ao final de um ano? A solução apresentada era a seguinte:
- no primeiro mês, haveria apenas um casal: o primeiro casal ainda não poderia se reproduzir.
- no segundo mês, o primeiro casal se reproduziria, havendo dois casais.
- no terceiro mês, o primeiro casal se reproduziria novamente, mas não o outro, havendo três casais.
- no quarto mês, os dois primeiros casais se reproduziriam, mas não o terceiro, havendo cinco casais.
- no n° mês, o número de casais seria a soma dos casais do mês $n-2$ com os casais do mês $n-1$.
À essa solução foi dada o nome de Sequência de Fibonacci pelo matemático francês Édouard Lucas. Para obtê-la, basta utilizar o mesmo raciocínio do problema apresentado:
Como a sequência de Fibonacci é obtida?
Para obtermos a sequência de Fibonacci, utilizamos a função $F(n)$, representada abaixo:
\[
F(n) =
\left\{
\begin{matrix}
0\,,\qquad\qquad\qquad\quad\,\ \ \,&&\mbox{se }n=0\,;\ \ \\
1,\qquad\qquad\qquad\qquad\,&&\mbox{se }n=1;\ \ \,\\
F(n-1)+F(n-2)&&\mbox{outros casos.}
\end{matrix}
\right.
\]
Importante: Antes de mais nada, gostaria de relembrar algo para não confundirmos: Em listas e funções, geralmente, nos referimos a seus elementos a partir do número 0.
Exemplo: para a sequência de Fibonacci [0, 1, 1, 2, 3, 5, 8…], o elemento F(0) é o primeiro, F(1) é o segundo e F(n) é o (n+1)° item da sequência. Parece um pouco complicado, mas logo você se acostuma. 🙂
Com isso, uma sequência gerada com n variando de 0 até 8, por exemplo, obtemos uma sequência com 9 itens!
Nós começamos a sequência de Fibonacci, por definição, com os números 0 e 1. O próximo elemento será, então, a soma do elemento anterior $(F(n-1))$ com o elemento anterior a ele $(F(n-2))$, ou seja, o terceiro elemento da sequência será $1+0=1$, o quarto será $1+1=2$, o quinto $2+1 = 3$ e assim por diante. Trata-se, então, de uma função recursiva. Para facilitar, uma imagem dos 11 primeiros elementos de $F(n)$:

No problema dos coelhos citado acima, a sequência descreve perfeitamente a quantidade de coelhos gerados em cada mês: no primeiro, seriam gerados $F(0)$ casal, ou seja, 0. No segundo, apenas $F(1)$ casal, ou seja, 1. No terceiro, 1. No quarto, 2. Já no quinto mês, por exemplo, seriam gerados $F(4)$ casais, ou seja, 3 casais, resultando em 8 casais (lembre-se do primeiro casal!):
Outras aplicações dos números de Fibonacci
Podemos aplicar os números de Fibonacci em diversas áreas, como na Matemática, na Ciência da Computação (falarei na terceira parte) e na Biologia. Algumas dessas aplicações interessantes são:
- No Triângulo de Pascal (utilizado para o estudo do Binômio de Newton), passando uma diagonal em cada linha, a soma dos números é equivalente a um elemento da sequência de Fibonacci:

- Podemos utilizar a sequência de Fibonacci para a conversão de milhas para quilômetros: se a medida estiver em milhas e está na sequência, basta convertê-lo utilizando o próximo número da sequência: 5 milhas $\approx$ 8 quilômetros, 8 milhas $\approx$ 13 quilômetros e assim por diante. De quilômetros para milhas, basta utilizar o elemento anterior. Isso ocorre pois o fator de conversão de Milha para Quilômetros (1.609) é aproximadamente igual à Proporção Áurea (1.618).
- Tais números podem também ser utilizados na Música (Fibonacci.ogg, na Wikipédia) e nas Artes Visuais.
Os números de Fibonacci estão em todos os locais da natureza (até mesmo no seu corpo) sob a forma da Proporção Áurea. Vou falar sobre ela na próxima parte, aguarde!
Ah, e se você sabe de alguma outra aplicação dos números de Fibonacci, deixe seu comentário! Enquanto isso, você pode me acompanhar pelo Twitter, Facebook ou pelo RSS para ler as próximas partes. A segunda parte já está praticamente pronta, logo eu a publico. 😉


Deixe um comentário